In the Spirit of Thébault I

Dr. Ray Viglione from Kean University and his undergraduate student Purna Patel found a variation of Victor Thébault's first problem that dealt with the configuration of squares built on the sides of a parallelogram.

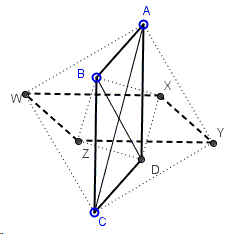
Given a parallelogram, the centers of the squares drawn on both sides of both diagonals form a parallelogram congruent to the original and rotated \(90^{\circ}\) about its center

Given a parallelogram, the centers of the squares drawn on both sides of both diagonals form a parallelogram congruent to the original and rotated 90 degrees about its center

The applet below serves to illustrate the problem and its solution:

As a backup for the GeoGebra applet, below is a plain diagram for a solution without words.

Given a parallelogram, the centers of the squares drawn on both sides of both diagonals form a parallelogram congruent to the original and rotated 90 degrees about its center - a PWW

References

  1. Purna Patel, Raymond Viglione, Proof Without Words: A Variation on Thébault's First Problem, The College Mathematics Journal, Vol. 44, No. 2 (March 2013), p. 135

Related material
Read more...

Thébault's Problems

  • Thébault's Problem I
  • Thébault's Problem II
  • Thébault's Problem III
  • Y. Sawayama's Lemma
  • Jack D'Aurizio Proof of Sawayama's Lemma
  • Y. Sawayama's Theorem
  • Thébault's Problem III, Proof (J.-L. Ayme)
  • Circles Tangent to Circumcircle
  • Thébault's Problem IV
  • A Property of Right Trapezoids
  • A Lemma on the Road to Sawayama
  • Excircles Variant of Thébault's Problem III
  • In the Spirit of Thebault I
  • Dao's Variant of Thebault's First Problem

    • |Contact| |Front page| |Content| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71536740