Cutting Triangle in Two by a Line through a Point
An interesting non-trivial problem has been posted at the math.stackexchange. An elegant solution was found by Dan Shved, a graduate student at the Moscow Institute of Physics and Technology. Dan's solution is interesting in that it was inspired by the properties of inversion, but, at the end of the day, did not need inversion for either construction or the proof of its validity.
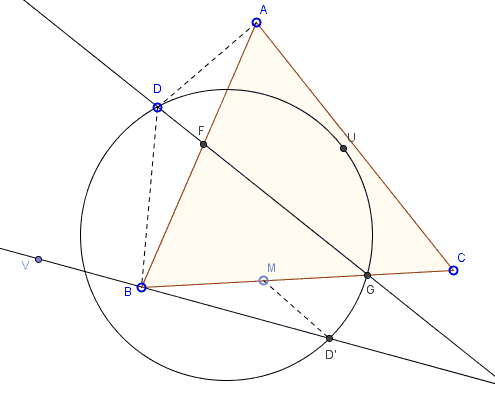
Given \(\Delta ABC\) and point $D$ in the plane of the triangle.

Draw a line through \(D\) that cuts the triangle into pieces of equal area.
(The applet below illustrates the construction.)
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Given \(\Delta ABC\) and point \(D\) in the plane of the triangle.

Draw a line through \(D\) that cut the triangle into pieces of equal area.
The construction below is easily adapted to solve the problem of cutting off a prescribed portion of the area of the triangle.
Construction
Assume, as in the diagram, that of the two triangles cut by the line \(CD\), the one that borders side \(BC\) has a larger area. If there is a solution, ot will cut the sides \(BC\) and \(AB\). Otherwise, the sought line will cross \(AB\) and \(AC.\) We assume the former case.
Find \(D'\) such that triangles \(BD'M\) and \(BAD\) are similar (with that particular order of vertices) and oriented in the same way, so that \(D'\) is \(BM,\) not over it.
Extend \(D'B\) beyond point \(B\) to get ray \(BV.\)
Find point \(U\) such that \(\angle D'UD = \angle VBA.\) Angles here are meant as oriented angles. To put it another way, point \(U\) should be on the "right" side of line \(DD'.\) Note that point \(U\) isn't uniquely defined, but it's OK. As will become clear, a particular choie of point \(U\) does not affect the construction.
Draw the circumcircle of \(\Delta DD'U.\)
Find \(G\) - the point of intersection of ray \(BM\) and arc \(DUD'.\)
We are done, line \(DG\) is the answer.
Proof
We will now prove that line \(DG\) that we have built really splits \(\Delta ABC\) into a triangle and a quadrilateral with equal areas.
By the construction, points \(D,\) \(D',\) \(G\) and \(U\) are concyclic. It follows that \(\angle D'GD = \angle D'UD.\) Also by the construction \(\angle D'UD = \angle VBA.\) So, \(\angle D'GD = \angle VBA.\) We can rewrite it like this: \(\angle D'GF = 180^{\circ} - \angle D'BF\) (here \(F\) is the point where \(DG\) meets \(AB,\) implying that \(BD'GF\) is a cyclic quadrilateral.
Let us introduce two transformations of the plane (technically, of the plane with addition of "point at infinity"). Transformation \(f\) will be an inversion with center \(B\) and radius \(r=\sqrt{|BG|\cdot |BF|}.\) Transformation \(g\) will be just a reflection in the bisector of \(\angle ABM.\) Let \(h = g \circ f\) be their composition. Because of our choice of \(r,\) \(h(F) = G\) and \(h(G) = F.\)
By a well known property of inversions, \(h\) maps the circumcircle of \(BD'GF\) into a straight line, because \(B\) maps to the point at infinity. Since \(h(F)=G\) and \(h(G)=F,\) this line is \(FG.\) It follows that \(h(D')\) belongs to the line \(FG.\)
By definition of an inversion, point \(f(D')\) lies on ray \(BD'.\) By the construction of \(D',\) \(\angle D'BM = \angle ABD.\) Therefore, \(g\) maps ray \(BD'\) into ray \(BD.\) It follows that \(h(D')=g(f(D'))\) lies on ray \(BD.\)
We have established that \(h(D')\) lies at the same time on line \(FG\) and on ray \(BD.\) Therefore, \(h(D')=D.\)
By definition of inversion \(f,\) we now have \(|BD'| \cdot |BD| = r^2 = |BG| \cdot |BF|.\) On the other hand, we have built point \(D'\) in such a way that \(\Delta BD'M\) is similar to \(\Delta BAD,\) so \(|BD'| \cdot |BD| = |BM| \cdot |BA|.\) It follows that \(|BG|\cdot |BF| = |BM| \cdot |BA|.\)
\(M\) is the middle of \(BC,\) so \(|BG| \cdot |BF| = \frac{1}{2} |BC| \cdot |BA|,\) which means that the area of \(\Delta BFG\) equals to half of the area of \(\Delta ABC,\) just as was required. Here taking \(M\) so that \(\frac{BM}{BC}=\alpha\) for a given \(0\lt\alpha\lt 1,\) solves the problem of cutting off a portion \(\alpha\) of the triangle's area.
This completes the proof. A day after posting his proof Dan added the following
Remark 1
Now that I think about it, one can simplify steps 1-5 of the proof and avoid the use of inversions. It goes like this: since points \(B,\) \(D',\) \(G\) and \(F\) are concyclic, \(\angle BD'G = \angle BFD.\) Also by construction \(\angle D'BG = \angle FBD.\) So triangles \(\Delta BD'G\) and \(\Delta BFD\) are similar, and \(|BD'|\cdot|BD|=|BF|\cdot|BG|.\) After this, we proceed to step 5.Remark 2
Leo Epstein has observed in private correspondence that my extention to ratios other than \(\frac{1}{2}\) is faulty. It only holds for points \(D\) outside \(\Delta ABC\); for internal points there are limitations. For example, for an equilateral triangle and \(D\) its center, the possible ratios range in \([\frac{4}{9},\frac{5}{9}].\)
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
71542598
