5x5 Square Grid and 5 Circes
In his book Mathematical Delights Ross Honsberger tells about a letter Professor Liong-shin Hahn received from a mathematics teacher. The latter posed to his student the following problem:
Given a 5×5 square grid.
Find five circles so that they pass through each of the 25 grid points at least once.
One of the students reported the following solution:
explaining that a straight line is nothing but a circle with an infinite radius. When the teacher insisted that the task was to find circles with finite radii, the student surprised the teacher with another diagram:
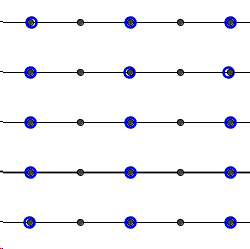
To teacher's objections the student rolled the diagram into a cylinder, making all circles of finite radius:
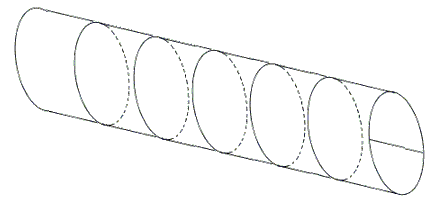
Naturally, that was not what the teacher had in mind. But what was it?
The applet below illustrates the problem. It may be helpful in finding the solution.
9 January 2013, Created with GeoGebra
(An HTML5 variant of this page appears on a separate page.)
References
- R. Honsberger, Mathematical Delights, MAA, 2004, 155-158
|Contact| |Front page| |Content| |Games and Puzzles| |Store|
Copyright © 1996-2015 Alexander Bogomolny
Solution
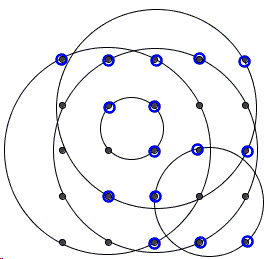
|Contact| |Front page| |Content| |Games and Puzzles| |Store|
Copyright © 1996-2015 Alexander Bogomolny
| 49551894 |
