Four Equal Incident Circles
What is this about?
A Mathematical Droodle
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyThe applet is supposed to suggest the folloing proposition:
Let there be four incident circles of equal radius. Four of the common tangents (as shown in the applet) form a quadrilateral. This quadrilateral is always cyclic.
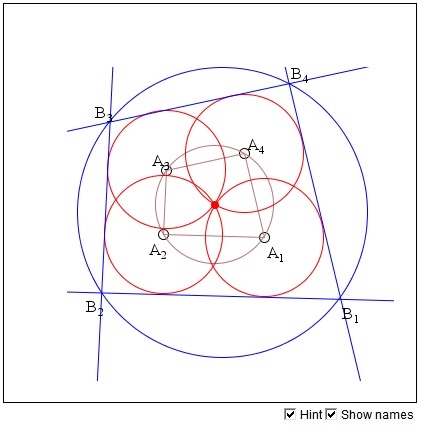
Denote the centers of the circles A1, ..., A4 and the corresponding vertices of the quadrilateral in question B1, ..., B4. Since the four circles have the same radius, the four points A1, A2, A3, A4 are concyclic and lie on a circle with center at the common point of the four given circles and radius equal to their common radius. Thus the quadrilateral A1A2A3A4 is cyclic. This in particular means that the opposite angles in A1A2A3A4 add up to 180°.
Turning to the quadrilateral B1B2B3B4, note that its sides are parallel to the corresponding sides of A1A2A3A4. For example, A1A2||B1B2. This is because the points A1 and A2 lie at the same distance from the common tangent B1B2 to the two circles. The corresponding angles of the two quadrilaterals are, therefore, equal. In particular, this implies that the opposite angles in B1B2B3B4 add up to 180°. The quadrilateral B1B2B3B4 is therefore cyclic.
References
- R. Honsberger, More Mathematical Morsels, MAA, 1991, pp. 36-37
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71534335
