Two Squares and Another Square
What is that about?
A Mathematical Droodle

Explanation

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Explanation

The applet suggests the following statment:

Given two squares ABCD and A'B'C'D' and a point P, let A1 = P + AA', B1 = P + BB', C1 = P + CC', and D1 = P + DD'. Then A1B1C1D1 is a square.

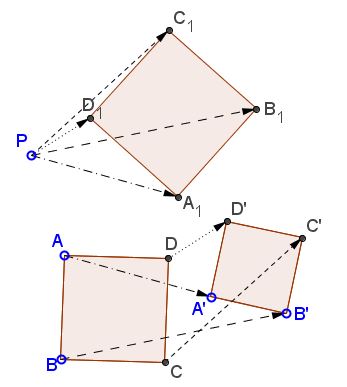
Theorem of directly similar figures, first variant

This is problem 46a from Yaglom. One solution follows from a more general statement about two directly similar figures.

References

  1. I. M. Yaglom, Geometric Transformations II, MAA, 1968

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72552102