Carpets in a Parallelogram

Points P, Q, R slide on the sides of parallelogram ABCD. Prove that, regardless of their position, the difference between the red areas and the blue area is constant.

Explanation

This is problem #53 from Which Way Did the Bicycle Go? where the problem is solved without mentioning The Carpets Theorem. The latter, however, is obviously relevant here and makes the proof more transparent.

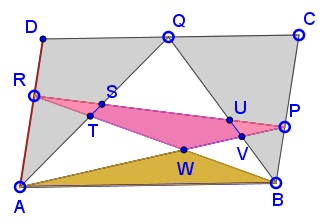
Forget for a moment about points P and R and subdivisions due to their presence. Let RED be the area of two triangles ADQ and BCQ. Clearly RED = Area(ABCD)/2. Let BLUE stand for the (blue) pentagonal area of STUVW. By the Carpets Theorem applied to the trapezoid ABPR we observe that the pink area and the orange area (see that the Hint box is checked) are equal:

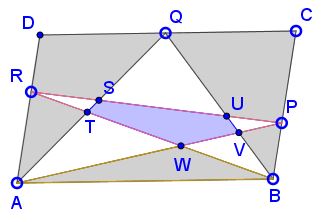
What we have to show (see that the Hint box is unchecked) is that

is independent of the position of the points P, Q, R. But in view of (1)

Q.E.D.

References

1. J. Konhauser, D. Velleman, S. Wagon, Which Way Did the Bicycle Go?, MAA, 1996, #52

• The Carpets Theorem
• Carpets in a Parallelogram
• Carpets in a Quadrilateral
• Carpets in a Quadrilateral II
• Square Root of 2 is Irrational
• Carpets Theorem With Parallelograms
• Two Rectangles in a Rectangle
• Bisection of Yin and Yang