Dividing a Segment into N parts:
Al-Nayrizi's Construction
A Mathematical Droodle: What Is This About?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Dividing a Segment into N parts:
Al-Nayrizi's Construction

The algorithm below has been included into Al-Nayrizi's commentary on Euclid's Elements. Euclid solves the problem of finding an N^th of a segment in Proposition VI.9. Al-Nayrizi's construction being simpler is clearly superior to Euclid's.

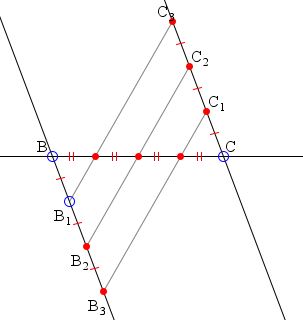
Let BC be a given segment to be divided into N parts. Draw two parallel lines through B and C and measure N equal segments on each: BB₁, B₁B₂, and so on, on one, and CC₁, C₁C₂, and so on, on the other pointing in different directions. Join the first of the points B with the last of C's and vice versa and join the rest by parallel lines. Those lines will cut BC into N equal segments.

• How to divide a segment into n equal parts
• Al-Nayrizi's Construction
• Besteman's Construction
• Besteman Construction II
• Dividing a Segment by Paper Folding
• Euclid's Segment Division
• The GLaD Construction
• The SaRD Construction
• Similar Right Triangles
• Divide Triangle by Lines Parallel to Base

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny