Angle Bisectors On Circumcircle

What is this about?
A Mathematical Droodle

Explanation

Related material
Read more...

Angle Bisector

  • Angle Bisector
  • Angle Bisector Theorem
  • All about angle bisectors
  • Angle Bisectors in Ellipse
  • Angle Bisectors in Ellipse II
  • Angle Bisector in Equilateral Trapezoid
  • Angle Bisector in Rectangle
  • Property of Angle Bisectors
  • Property of Angle Bisectors II
  • A Property of Angle Bisectors III
  • External Angle Bisectors
  • Projections on Internal and External Angle Bisectors
  • Angle Bisectors in a Quadrilateral - Cyclic and Otherwise
  • Problem: Angle Bisectors in a Quadrilateral
  • Triangle From Angle Bisectors
  • Property of Internal Angle Bisector - Hubert Shutrick's PWW
  • Angle Bisectors Cross Circumcircle
  • For Equality Choose Angle Bisector

    • |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    The applet attempts to suggest the following problem [Tao, pp. 50-51]:

    ABC is a triangle that is inscribed in a circle. The angle bisectors of A, B, C meet the circle in D, E, F, respectively. Show that AD is perpendicular to EF.

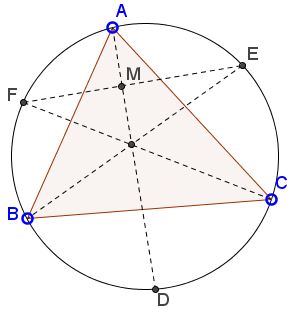
    angle bisectors interset the circumcircle - problem

    We'll concentrate on ΔFIM.

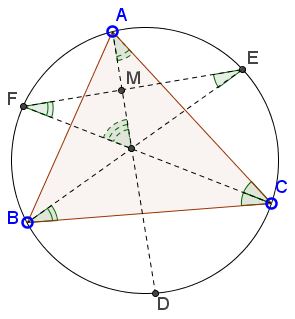
    angle bisectors interset the circumcircle - solution

    By a theorem of the inscribed angles,

    ∠IFM = ∠CFE = ∠CBE = ∠B/2.

    By a the theorem of the secant angles (or with the help of the Exterior Angle Theorem),

    ∠FIM = ∠ACI + ∠CAI = ∠C/2 + ∠A/2.

    It follows that in ΔFIM, angles at F and I add up to 90°:

    ∠A/2 + ∠B/2 + ∠C/2 = 180°/2 = 90°.

    We conclude that the remaining angle at M is necessarily right.

    References

    1. T. Tao, Solving Mathematical Problems, Oxford University Press

    |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71941605