Acute Angle Bisectors in a Right Triangle

The applet below illustrates problem 4 from the 1995 British Mathematical Olympiad.

Triangle ABC has a right angle at C. The internal bisectors of angles BAC and ABC meet BC and AC at P and Q respectively. The points M and N are the feet of the perpendiculars from P and Q to AB. Find angle MCN.

Buy this applet What if applet does not run?

Solution

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2015 Alexander Bogomolny

Triangle ABC has a right angle at C. The internal bisectors of angles BAC abd ABC meet BC and AC at P and Q respectively. The points M and N are the feet of the perpendiculars from P and Q to AB. Find angle MCN.

Buy this applet What if applet does not run?

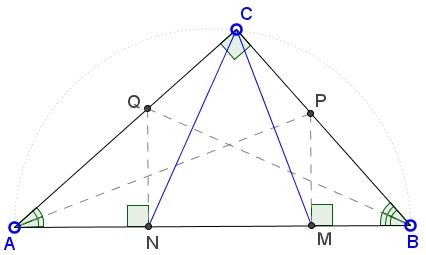
Since AP is an angle bisector, ∠CAP = ∠BAP. The two right triangles CAP and MAP share a hypotenuse and have equal acute angles, implying ΔCAP = ΔMAP. It follows that CP = PM, making ΔCPM isosceles. Also, AC = AM and the quadrilateral ACPM is a kite, so its diagonals are perpendicular: AP ⊥ CM.

Similarly, ∠CNQ = ∠BCN, triangle CNQ is isosceles, CQ = CN and CN ⊥ BQ.

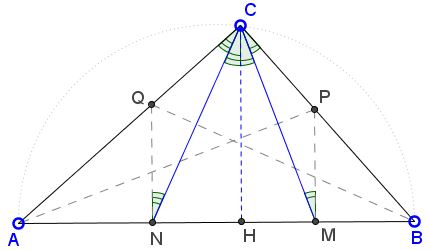
Let CH be the altitude to AB. Then, since CH||PM||QN, ∠HCM = ∠CMP = ∠BCM and also ∠HCN = ∠CNQ = ∠ACN. It follows that

∠MCN	= ∠HCM + ∠HCN
	= (∠HCM + ∠BCM + ∠HCN + ∠ACN)/2
	= ∠ACB/2 = 45°.

This solves the olympiad problem.

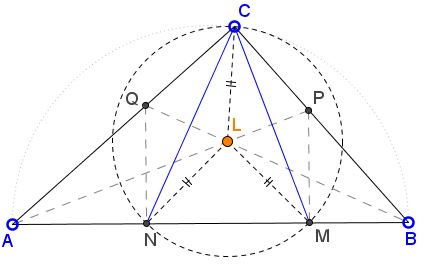
However, the configuration conceals additional features. One is that L, the intersection of AP and BQ, i.e., the incenter of ΔABC, is the circumcenter of ΔCMN. Indeed in a kite, the long diagonal passes through the midpoint of the short diagonal, meaning that, in our case, AP is the perpendicular bisector CM, while BQ is the perpendicular bisector of CN. It then also follows that ∠MLN = 90°. (There are several additional features.)

References

1. T. Gardiner, The Mathematical Olympiad Handbook, Oxford University Press, 1997.

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2015 Alexander Bogomolny